全80ページ!玉井式『図形の極み』体験版テキストをタダでGETする方法とは

- 玉井式「図形の極み」の問題内容
- 体験版問題集を無料で手に入れる方法
ゆくゆくは中学受験を考えているんだけど、低学年のうちは何もしなくて良いのかしら?
中学受験の準備に最適な教材に出会ったのでご紹介しますね。
この春、小学校2年生になった娘は、4歳の頃からずっと公文(くもん)に通っています。
>>その時の失敗談はこちら
公文では算数と英語を受講しており、娘もとても楽しく通っています。
ただ、公文は完全に暗記学習です。
たし算の概念を教えることなく、ただただ答えを暗記していきます。
英語はそれで良いかもしれませんが、算数はほぼ計算問題だけをひたすら繰り返すばかり。
公文での学習経験がない私は、ただの暗記学習ではなく、思考力を養う勉強をしてほしいと思うようになりました。
そして色々と調べていく中で、『玉井式』に出会ったんです。
\2年間継続受講中の娘の口コミです/

玉井式『図形の極み』の問題を10枚の写真で解説します

体験版教材の入手方法は、次の章で紹介します。
まずは、玉井式『図形の極み』の問題を見てみましょう。
体験版では、『立体図形』と『展開図』の問題のうち、10級~7級の問題の一部を学習できます。
実際には
- 平面図形
- 立体図形①
- 立体図形②
- 展開図
- 角度
- 垂直と並行
- 比
- 動く図形
の8項目に分けて、それぞれ10級~1級までをレベル別に学習できるようです。
ここからは、小2の娘が取り組んだ様子とあわせて問題を紹介していきます。
玉井式『図形の極み』10級問題
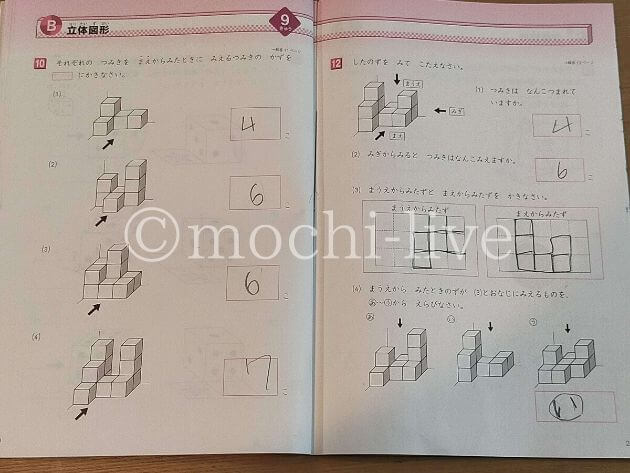
これが一番やさしい10級の「立体図形」問題です。
『え、これで?』と思いませんか?
左は、サイコロを☆印まで転がした時の「うえのめ」を求める問題。
右は、絵のつみきを前から見た時にみえるつみきの数をもとめる問題です。
我が家は「こどもチャレンジ」や「Z会」、「スマイルゼミ」や「公文」といった幼児教育を経験してきましたが、こんなにも思考力を問う問題を見たのは初めてです!
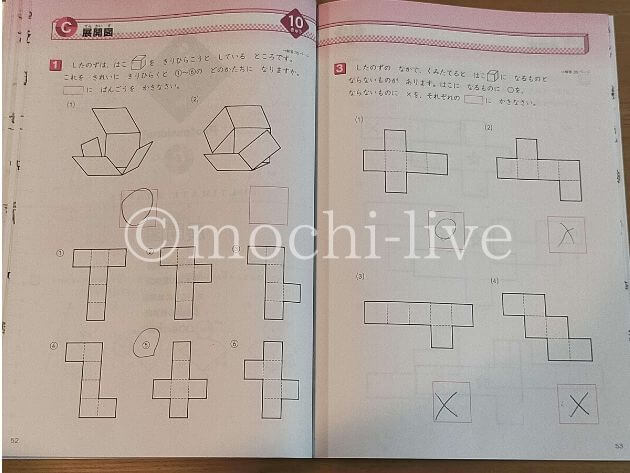
そしてこちらは同じく10級の「展開図」の問題。
左は、箱を切り開いた時どうなるかを求める問題です。
答えの番号を書かなければいけないのですが…娘は問題の意図が理解できていないようですね。。
右は、さっきとは逆に、組み立てた時に箱になるものを求める問題です。
どちらも、頭の中でイメージする力が必要ですね。
玉井式『図形の極み』9級問題
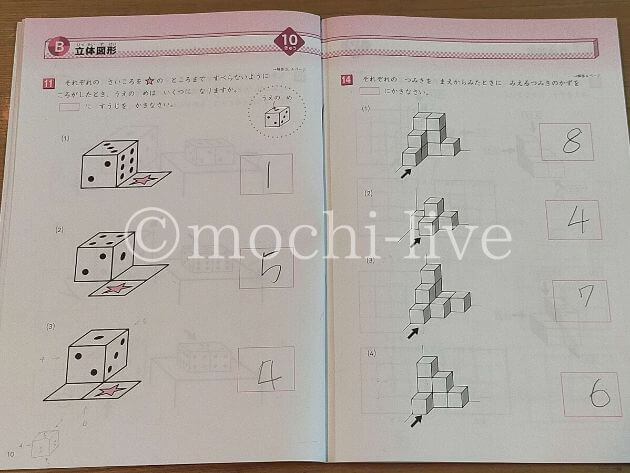
こちらは1つレベルが上がった9級の「立体図形」問題です。
左は、まえから見た時に見えるつみきの数を求める問題。
凹凸が少し複雑になったものの、10級で似たような問題をやっていたので、娘も難なく解けました。
右は、一気にレベルアップした気がします。娘も間違えているのがわかりますか?
今まで前からだけでしたが、上や右から見た場合の数をさらっと聞いた後、まえから見た図を書かせる問題です。
まえから見た数を答えられるのに、その時の図を書いてと言うと、一気に娘は混乱していました。
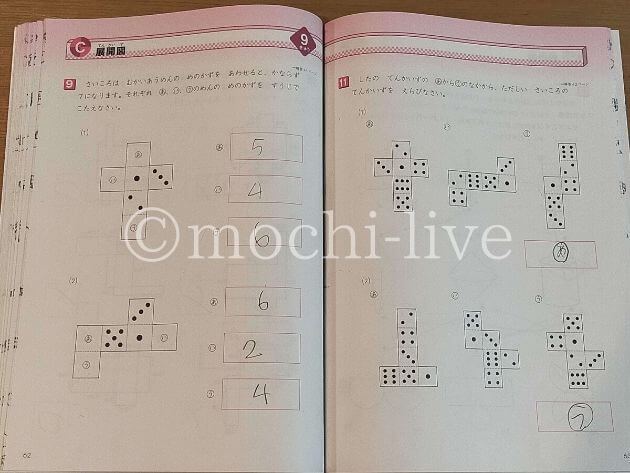
そしてこちらは9級の「展開図」の問題です。
10級では、白紙の箱の展開図でしたが、9級になるとサイコロの目が出てきます。
左は、組み立てた時に㋐~㋒に入るサイコロの目の数を求める問題。
『サイコロは向かい合うめの合計が7になる』ことは10級の立体図形問題でも取り扱ってきました。
ですが、それを展開図から求めさせるだなんて…すごくないですか?
右はさらに難問です。
正しいサイコロの展開図を求める問題なのですが、どれも単なる立方体の展開図としては正しいんです!
ただ、『サイコロの』とつくと、むかい合うめの数を考えなければなりません。
あまりにも良問が多すぎて、この辺りから私も『図形の極み』にのめり込むようになりました。

玉井式『図形の極み』8級問題
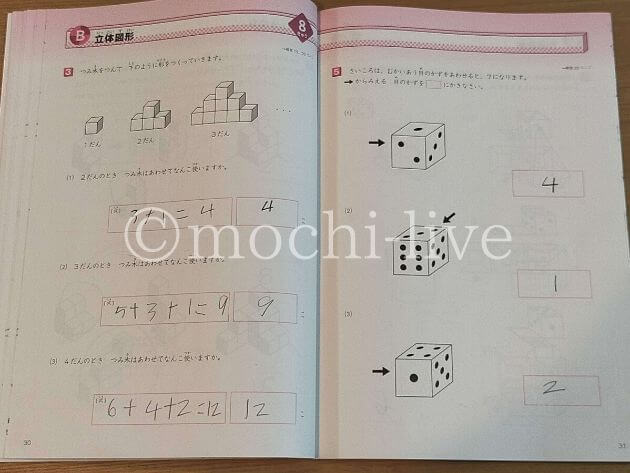
こちらは、8級の「立体図形」問題です。
左は、つみきを絵のように1段ずつ高く積み上げていった時のつみきの数を求める問題。
絵は3段までしかありませんが、3つ目の問題は4段重ねた時のつみきの総数を問われています。
娘、間違っていますね;
ここは、1段増えるごとに一番下の段が2こずつ増える、ということに気づかなければなりません。
右は、矢印の目の数を問う問題で、ここまで進めてきた娘は「なんでこんな簡単な問題でるんだろうね」と言っていました(笑)。
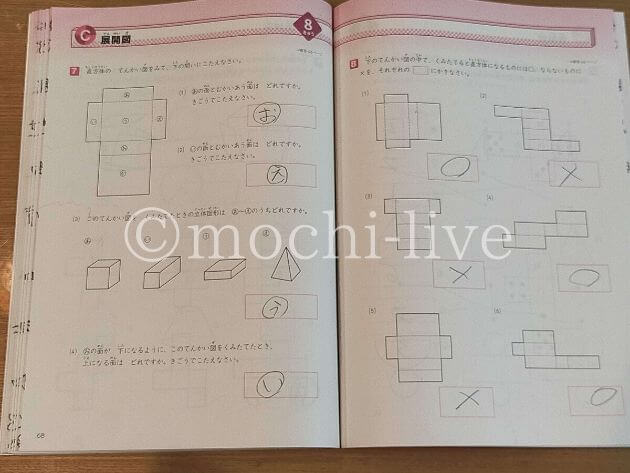
8級「展開図」の問題では、サイコロとは違う立体図形がでてきました。
左は、直方体の展開図を元に、むかい合う面を問う問題です。
娘も間違えていますが、最後の問題では、指定された面を下にして組み立てた時の上の面を聞いています。
展開図を元に頭の中で組み立て、さらにその立方体を動かさなければならないというイメージ力…大人でも厳しくないですか?
右は、いろんな形の展開図を組み立てて、直方体になるものに〇をつける問題です。
私、この手の問題がすごく苦手でした。。。
各面の大きさの違いに注意して組み立てるイメージができる娘に、感動を覚えましたね。
こうした問題のおかげで、娘のイメージ力も伸びてきたと感じます。

玉井式『図形の極み』7級問題
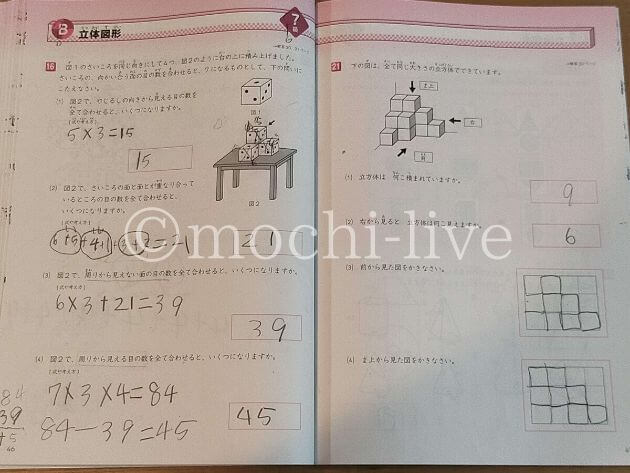
7級「立体図形」の問題は、中学受験を思わせるような、問題の意図を理解し本質を見抜く力が問われます。
左は、4つのサイコロを同じ向きに絵のように重ねた時、
- 矢印の方向から見える数の和
- サイコロの面が重なっている数の和
- 周りから見えない数の和
- 周りから見える数の和
を問う問題です。
「レベル高っ!」と思わず声に出してしまいました。
娘には最初自力で解かせたので、写真の通り独特な解き方をしています。
4つ目の問題は全く歯が立たなかったので、何度も説明して一緒に解きました。
それでもしっくりきていないようだったので、ついには紙でサイコロを作っちゃいました(笑)。

サイコロを1つずつ増やしていき、どこが見えなくなるのか、その時の数の和はどう考えていくのかをクイズ形式で出していきました。
サイコロ3つまではすんなり答えられるのに、なぜか4つになると最後の答えにつまります…
私の教え方が悪いようです;
そして右の問題は、矢印の方向から見た時のサイコロの数と図を書く問題。
8級でもでてきましたが、娘はとても苦手なようです。
前からみた図以外は全て間違えていますね。。
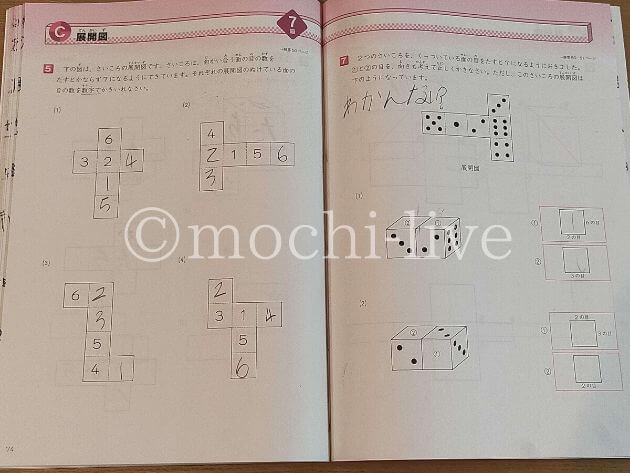
7級「展開図」の問題は、サイコロを組み立てた時の目の数を問う問題です。
左は、展開図のまま考える問題。
娘は展開図のまま考えるのは得意なようです。
どことどこの面がツイになるのかがわかっているのですね。
右は、展開図ではなくサイコロの状態で指定の目の数を求める問題です。
要領は左ページの問題と同じはずなのですが、サイコロの状態になるとわからなくなったようです。
問題の出し方で、捉え方がこうも変わってしまうのですね。

玉井式『図形の極み』の映像学習

実は私、1冊すべて終わるまで、すっかり
「映像学習」の存在を忘れていたのです…
なのでここまで、娘はノーヒントで全て自力で取り組み、わからなかった問題を私が必死で教えていました。
そして体験版教材が届いてから2週間後に、担当の方からお電話をいただき
「映像学習の方は無事ログインできましたか?」
と言われて、ようやく存在を思い出したのです…
素直に見れていない旨を伝えると、なんと、さらに2週間、無料視聴を延長してくださったのです!!
な、なんてお優しい…
そして、週末に初めてログインをして見てみると、、、
子ども目線の動画がなんともわかりやすいT_T
映像では、答えを言うのではなく、アプローチの方法を、子どもに話しかける感じで教えてくれました。
例えば、私が教えるのに一番苦労した、7級の立体図形の問題。
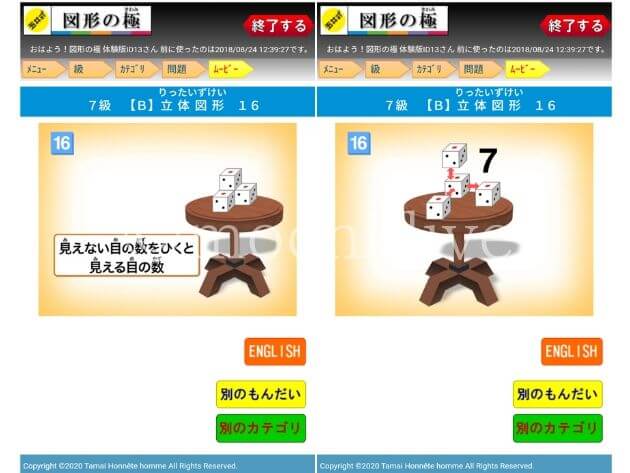
4つのサイコロを重ねておいた時の「見える目の数の和」を求める問題では、
- 見えていない目をアニメーションで見せる
- 『全体ー見えない目の数=見える目の数』になるイメージを膨らませる
という方法でヒントを出してくれ、娘も思わず「わかりやすい!」と声に出して喜んでいました。
みなさんは、私のような失敗はせず、最初から映像と合わせて取り組んでくださいね。
タダで玉井式『図形の極み』問題集を手に入れる方法とは

色々調べていく中で、私は「総合学習館 イング」から資料請求をしました。
玉井式の教材に特化して取り組んでおり、Gakkenグループなので、変な売り込みはされないと思ったからです。
実際に、一言も「売り込み」らしい言葉を聞くことはなく、とても親切に対応いただきました。
資料請求って、過剰な押し売りをされないか、ちょっと不安なんですよね。。
ただ、 普通に資料請求しただけでは、数枚のちらしだけしか届かなかったんです。

そして1週間後に到着確認の電話があったのですが、『教材の中身を見てみたかった』と話すと、すぐに見本教材を送ってくれました!

しかも、前項で紹介した『図形の極み』の問題集だけでなく、映像講義も2週間、無料視聴させてくださったんです!
80ページもある冊子を無料でいただけるなんて、すごく得した気分でした。
その後も、一切勧誘されることはなく、こちらの質問に丁寧に応えてくださり、とても印象が良かったです。
体験教材をお送りいただいた際にも、こんなお手紙をくださいました。

他のサイトから玉井式の資料請求をしたことがないのでわかりませんが、イングの担当の方は拍子抜けするほどあっさりしていて営業感はなく、とても好印象でした。
メールフォームに「見本教材が見たい」と書いておくと、1度目で送ってくれると思います。
玉井式の教材は多くの学習塾で取り入れられています

『玉井式』では、グローバル社会を生き抜くためには、次の3つの力が必要だと説いています。
- 自分の頭で考え、その考えを言葉にする表現力
- 理解を深め、解決策を探るための思考力
- 想定外の事態でも臨機応変に行動できる判断力
玉井式ではこれらの基盤となる「イメージング力」を育てて、公式を使わずに公式を生み出すような能力育成学習を行います。
先ほどの体験版教材を見てみれば、一目瞭然ですよね。
実際に、玉井式の教材のレベルは高く評価されており、多くの受験指導校で取り入れられています。
この導入実績が玉井式教材の質の高さを証明していますよね。
玉井式『図形の極み』を体験して感じるメリット

今回、玉井式の『図形の極み』体験版を経験してみて、特に良かったと思うのは次の7点です。
- 1問の解説動画が短く、子どもも集中して取り組める
- 教科書にはない難易度の高い問題に取り組める
- アニメーションが豊富でイメージしやすい
- 自分で考えるから、わかった時に楽しい
- 自然と想像させる問題設計になっている
- 学年に関係なくレベルアップができる
- 暗記ではなく自分で考える力がつく
中学・高校受験の合格のカギは図形問題の得点力です。
中学入試における正答率の低い問題No.1は図形問題だそうです。
また、高校入試では図形問題が1番出題率の高い分野となっています。
私自身、高校入試を経験していますが、図形問題が特に苦手でした。
立方体を切った断面図を求める問題が特に苦手で、頭の中で切ったあとの図形をイメージすることができなかったんです。
玉井式『図形の極み』は、いろんなパターンのアニメーションで想像力を刺激してくれます。
「見えない部分を想像する力」や「物事を多方面から考える発想力」が身に着くと感じました。
玉井式『図形の極み』問題集を無料で手に入れる方法のまとめ

玉井式『図形の極み』の問題を写真付きで紹介してきました。
現在、スマイルゼミと公文を受講中の小学2年の娘にも、少し難しかったようです。
ですが、映像コンテンツと合わせて学習すると、一気にイメージが湧き、とても楽しいと言っていました。
玉井式『図形の極み』に興味が湧いた方は、ぜひ資料請求をしてみてください。
もちろん無料ですし、イングからしつこい勧誘をされることもありませんでしたよ。
メールフォームでの請求なので、一番最後の『ご質問など』の欄に、「見本教材を見て検討したい」と一言添えると良いと思います。
百聞は一見に如かず!
ぜひ体験教材で、お子さまの実力試しをしてみてください。
- 図形の極みで思考力とイメージング力を伸ばす!
- 資料請求でP80の体験版教材をもらいました
2021年3月値上がり予定です!
資料請求時に『見本教材をみて検討したい』と伝えるとよいと思います。
\イングの受講料はこちらから/

\娘の正直な口コミです/



























